《算法图解》读书笔记第二章选择排序

内存的工作原理

计算机内存就像是很多抽屉的集合体，每个抽屉都有地址。fe0ffeeb是一个内存单元的地址。

需要将数据存储到内存时，你请求计算机提供存储空间，计算机给你一个存储地址。需要存储多项数据时，有两种基本方式——数组和链表。

数组和链表

存储方式：

数组中的元素在内存中是相连的。
链表中的元素可存储在内存的任何地方。链表的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在一起。

分配内存：

使用数组时有时就会遇到这样的情况。假设你要为数组分配10 000个位置，内存中有10 000个位置，但不都靠在一起。在这种情况下，你将无法为该数组分配内存！
链表相当于说“我们分开来坐”，因此，只要有足够的内存空间，就能为链表分配内存。

添加元素：

在数组中添加新元素可能很麻烦。如果没有了空间，就得移到内存的其他地方，因此添加新元素的速度会很慢。
在链表中添加元素很容易，只需将其放入内存，并将其地址存储到前一个元素中。

在中间插入元素：

使用链表时，插入元素很简单，只需修改它前面的那个元素指向的地址。
而使用数组时，则必须将后面的元素都向后移。

删除元素：

链表删除元素时，只需修改前一个元素指向的地址即可。
而使用数组时，删除元素后，必须将后面的元素都向前移。

随机读取第n个元素：

需要随机地读取元素时，数组的效率很高，因为可迅速找到数组的任何元素。
在链表中，元素并非靠在一起的，你无法迅速计算出第n个元素的内存地址，而必须先访问第一个元素以获取第二个元素的地址，以此类推，直到访问第n个元素元素。

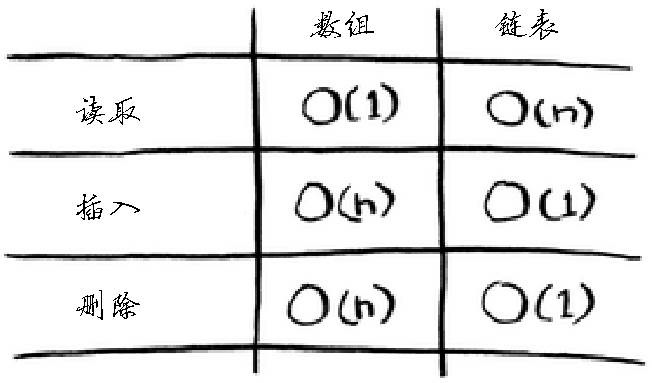
常见的数组和链表操作的运行时间：

选择排序

比如要将乐队按照播放次数排序，可以先找出作品播放次数最多的乐队，将该乐队添加到一个新列表中，再找出播放次数第二多的乐队，继续这样做，将得到一个有序列表，这就是选择排序。

随着排序的进行，每次需要检查的元素数在逐渐减少，最后一次需要检查的元素都只有一个。平均每次检查的元素数为1/2 × n ，因此运行时间为O(n × 1/2 × n)。但大O表示法省略1/2这样的常数，因此可以写作O(n²)。

选择排序是快速排序的基石。

先编写一个用于找出数组中最小元素下标的函数：

def find_smallest_index(arr):
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < arr[smallest_index]:
            smallest_index = i
    return smallest_index

然后使用这个函数来编写选择排序算法：

def selection_sort(arr):
    new_arr = []
    for i in range(len(arr)):
        index = find_smallest_index(arr)
        new_arr.append(arr.pop(index))
    return new_arr

小结

计算机内存犹如一大堆抽屉。
需要存储多个元素时，可使用数组或链表。
数组的元素都在一起。
链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
数组的读取速度很快。
链表的插入和删除速度很快。
在同一个数组中，所有元素的类型都必须相同（都为int、double等）。