NP完全问题
NP完全问题是多项式复杂程度的非确定性问题。
NP完全问题无处不在!如果能够判断出要解决的问题属于NP完全问题就好了,这样就不用去寻找完美的解决方案,而是使用近似算法即可。但要判断问题是不是NP完全问题很难,易于解决的问题和NP完全问题的差别通常很小。
虽然判断问题是不是NP完全问题很难,但还是有一些蛛丝马迹可循的:
- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是NP完全问题。
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
- 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题。
- 如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题。
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
近似算法
面临NP完全问题时,最佳的做法是使用近似算法。
判断近似算法优劣的标准如下:
- 速度有多快;
- 得到的近似解与最优解的接近程度。
贪婪算法
贪婪算法的做法:每步都选择局部最优解 ,最终得到的就是全局最优解。
贪婪算法易于实现、运行速度快,是不错的近似算法。
贪婪算法案例
教室调度问题
问题描述:根据某课程表,如何将尽可能多的课程安排在某间教室上,上课时间不能冲突。
贪婪算法的做法如下:
- 选出结束最早的课,它就是要在这间教室上的第一堂课。
- 接下来,必须选择第一堂课结束后才开始的课。同样,你选择结束最早的课,这将是要在这间教室上的第二堂课。
- 重复这样做就能找到最优解。
背包问题
问题描述:往一个可装35磅的背包装东西,可以装的东西以下三种:
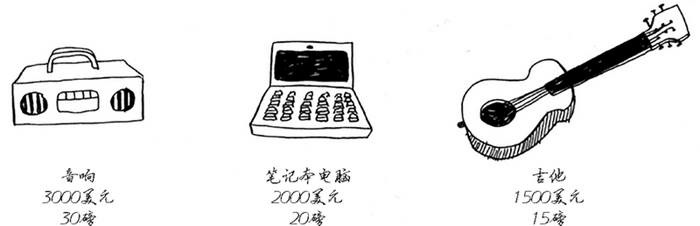
贪婪策略的做法如下:
- 拿可装入背包的最贵商品。
- 再拿可装入背包的最贵商品,以此类推。
在这个问题中,贪婪策略不能获得最优解,但非常接近。
集合覆盖问题
问题描述:假设你办了个广播节目,要让全美50个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠。现有广播台名单如下:
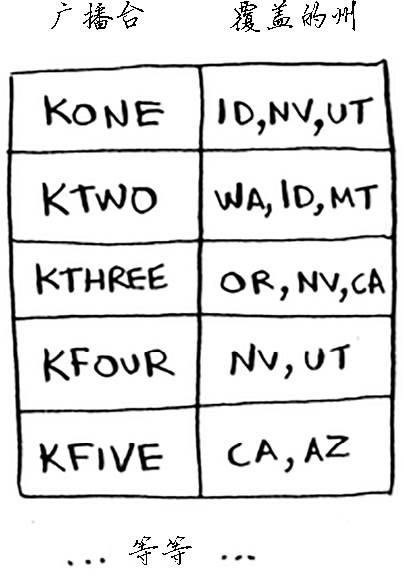
精确求解:如果列出每个可能的广播台集合,相当于计算幂集 (power set)。可能的子集有2n个。
贪婪算法可化解危机!使用下面的贪婪算法可得到非常接近的解:
- 选出这样一个广播台,即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州,也没有关系。
- 重复第一步,直到覆盖了所有的州。
在这个例子中,贪婪算法的运行时间为O(n2),其中n为广播台数量。
旅行商问题
问题描述:旅行商需要前往5个不同的城市,他需要找出前往这5个城市的最短路径。
精确求解:要计算每条可能的路径。可能的路线有n!条,n为城市数。如果涉及的城市很多,根本就无法找出旅行商问题的正确解。
近似求解:
- 随便选择出发城市,然后每次选择要去的下一个城市时,都选择还没去的最近的城市。
- 重复第一步。
练习题
问题1:你在一家家具公司工作,需要将家具发往全国各地,为此你需要将箱子装上卡车。每个箱子的尺寸各不相同,你需要尽可能利用每辆卡车的空间,为此你将如何选择要装上卡车的箱子呢?请设计一种贪婪算法。使用这种算法能得到最优解吗?
答:每次选择体积最大的,不能得到最优解。
问题2:你要去欧洲旅行,总行程为7天。对于每个旅游胜地,你都给它分配一个价值——表 示你有多想去那里看看,并估算出需要多长时间。你如何将这次旅行的价值最大化?请设计一种贪婪算法。使用这种算法能得到最优解吗?
答:每次选择一个单位时间的价值(价值/时间)最大的地方,不能得到最优解。
问题3:快速排序是不是贪婪算法?
答:不是
问题4:广度优先搜索是不是贪婪算法?
答:不是
问题5:狄克斯特拉算法是不是贪婪算法?
答:是
问题6:有个邮递员负责给20个家庭送信,需要找出经过这20个家庭的最短路径。请问这是一个NP完全问题吗?
答:是
问题7:在一堆人中找出最大的朋友圈(即其中任何两个人都相识)是NP完全问题吗?
答:是
问题8:你要制作美国地图,需要用不同的颜色标出相邻的州。为此,你需要确定最少需要使用多少种颜色,才能确保任何两个相邻州的颜色都不同。请问这是NP完全问题吗?
答:是
小结
- 贪婪算法寻找局部最优解,企图以这种方式获得全局最优解。
- 对于NP完全问题,还没有找到快速解决方案。
- 面临NP完全问题时,最佳的做法是使用近似算法。
- 贪婪算法易于实现、运行速度快,是不错的近似算法。