《算法图解》读书笔记第九章动态规划

动态规划将问题分为效问题，先解决子问题，再逐步解决大问题。

在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。

设计动态规划解决方案的小贴士：

问题描述

往一个可装4磅的背包装东西，可以装的东西以下三种：

动态规划的做法

对于背包问题，你先解决小背包（子背包）问题，再逐步解决原来的问题。

每个动态规划算法都从一个网格开始，背包问题的网格如下：

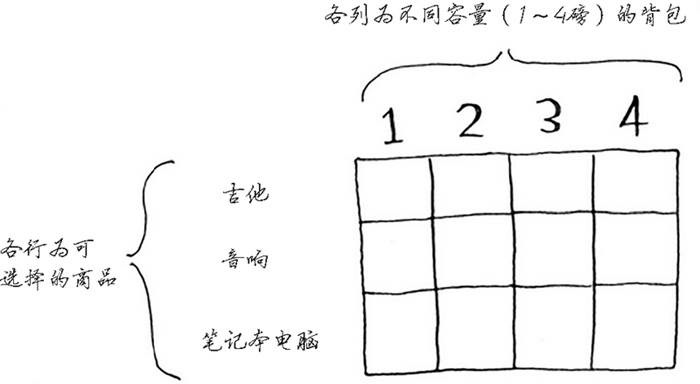
网格最初是空的。你将填充其中的每个单元格，网格填满后，就找到了问题的答案！

计算每个单元格的价值时，使用的公式都相同。这个公式如下：

FAQ

问题1：沿着一列往下走时，最大价值有可能降低吗？

答：不可能。每次迭代时，你都存储当前的最大价值。最大价值不可能比以前低！

问题2：行的排列顺序发生变化时结果将如何。

答：各行的排列顺序无关紧要。

问题3：可以逐列而不是逐行填充网格吗？

答：就这个问题而言，这没有任何影响，但对于其他问题，可能有影响。

问题4：增加一件更小的商品将如何做呢。假设加入一条项链，它重0.5磅，价值1000美元。

答：由于项链的加入，需要考虑的粒度更细，因此必须调整网格，横坐标以0.5磅为一个单位

问题5：如果可以拿商品的一部分，比如大米，这时如何使用动态规划来处理？

答：不能使用动态规划。可以使用贪婪算法，首先，尽可能多地拿价值最高的商品；如果拿光了，再尽可能多地拿价值次高的商品，以此类推。

问题6：如果两个商品互相依赖该如何建模。比如将吉他加入“背包”后，音响将更“便宜”。

答：没办法建模。仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。

问题7：计算最终的解时会涉及两个以上的子背包吗？

答：根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。

问题8：最优解可能导致背包没装满吗？

答：可能。

问题描述

fish和vista这两个单词哪一个和hish更像。

问题分析

我们要找出两个单词的最长公共子串。找出hish和fish都包含的最长子串，以及hish和vista的最长子串，然后比较两个最长子串的长度。

动态规划

动态规划的单元格中的值通常就是要优化的值。在这个例子中，这很可能是一个数字：两个字符串都包含的最长子串的长度。

用动态规划来找出两个单词的最长公共子串的公式：

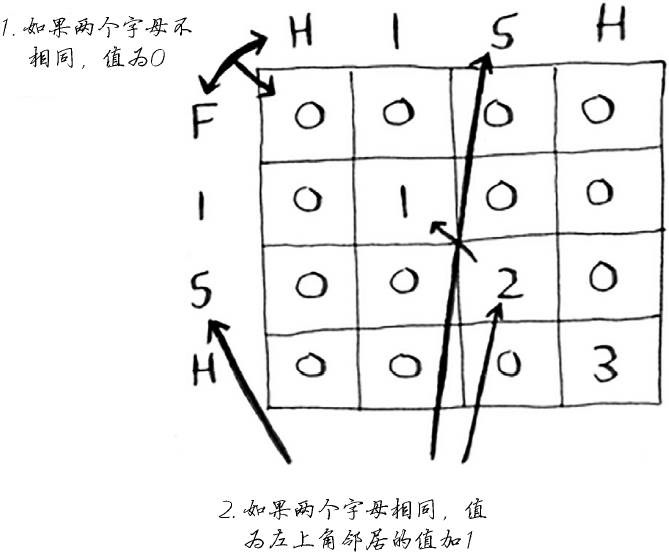
伪代码如下：

if word_a[i] == word_b[j]:
    cell[i][j] = cell[i-1][j-1] + 1
else:
    cell[i][j] = 0

动态规划找出两个单词的最长公共子序列的公式：

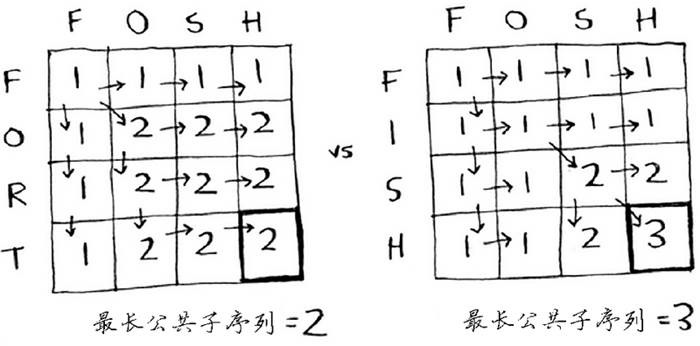
伪代码如下：

if word_a[i] == word_b[j]:
    cell[i][j] = cell[i-1][j-1] + 1
else:
    cell[i][j] = max(cell[i-1][j], cell[i][j-1])